90. Resonance Direction -Down bowing vs Up bowing-

[ 12/26/2019 ]     Labels:  70.Resonance Direction

 
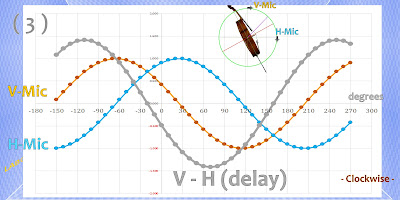
Resonance directions on cello were briefly measured at A-G chromatic semitones on A-string and also D-C semitones on D-string comparing with 'steel pipe endpin 300mmL on floor' and 'without endpin', down-bowing and up-bowing.
(1)The results can be divided into two groups; [group-a]stable, clear tendency in resonance direction, [b]diverse, taking various resonance directions. The reason of [b] is not enough clear now, probably because of the factors such as multi phases even during the target semitone, difficulties in judgement of delay/waveform, complexity, vulnerability, interruptions by external effects. Differences between down-bowing and up-bowing were unclear either.
(2)According to the frequency transition, as a long-tern viewpoint, the resonance direction seems rotating. The angle rather drifts near around 0 degree on D string, however unlikely D, the angle seems spreading/rotating wide-angle on A string.
(3)There might be a possibility that an endpin narrows down the angle range of resonance. These results might reek us a secret of the body of violin-family instruments that has been probably designed originally as being able to resonate for all-round directions.
Resonance direction measurements will be gone on by switching the examinee-instrument to CELLO-1.

Cello-2(115歳・ドイツ製)について、スチールパイプエンドピン300mmL(床置)とエンドピン無(スタンド置)で、各々ダウンボーイングとアップボーイングにて、A線及びD線上の各半音ごとの振動の方向を計測した。測定データ数は十分とは言い難いが、次の傾向が見られた。
(1)安定して独自の振動方向を示す音グループ[a]と、多様な方向を示す音グループ[b]の２グループに分かれた。
[a]は、A線上では H C# D# E F#、D線上では E F F# G G# A# であり、
[b]は、A線上では A D F G、D線上では D D# H であった。多様な方向を示す理由は、今後さらに調べる予定であるが、例えば、一つの半音域の中に多様な振動形態を持つ・位相の計算が難しい(判別しにくい)・振動波形が交錯したりつぶれたりしている・何某かの外的影響を受けやすい、などが考えられる。ダウン/アップボーイングで違いが見られるのは[b]グループである。
(2)大きく見ると、周波数の変化とともに振動方向が回転(ローテート)しているように見える。D線域では胴体の輪切り方向(=低角度)に振動することが多く回転周期も長いが、一方 A線域では 激しく変化しているように見える。
(3)エンドピン有り/無しで比較するとエンドピン無しの場合の方がわずかではあるが、多様な振動方向を取っているようにも感じられる。バイオリン属の胴体の形状・構造はそもそも多様な振動・共鳴を取りうるように設計されているのかもしれない。
次の投稿では、Cello-1を使ってもう少し多くのデータを調べてみる。

90. Resonance Direction - Calculation -

[ 12/13/2019 ]     Labels:  70.Resonance Direction

 
Each chromatic tone of cello has own characteristic waveform or the resonance direction. This phenomenon depends on the each individual instrument issue however at the same time, probably the common truth based on the structure.
Now new better-accuracy measurements are launched. The plan image is as follows ;
1.The resonance direction will be indicated as a counterclockwise angle(degrees) from the round slice level of cello body.
2.Two microphones placed at vertically and horizontally catch the cello sound wave according to each distance with the eligible delay. They are calculated as (Microsoft Excel function:) '=COS( )' or '=SIN( )'. The delay period is described as a sine curve too. This means the resonance direction can be described like '=ACOS(delay/(phase/2))...'.
3.Actually cello is not usually played at the angle of 45 degrees from the floor, but around 65 degrees. This deviation should be compensated and embedded in the calculation.
4.Overview will come out soon, but some special tones with like collapsed or complicated wave pattern will be took place a detailed testing later.
5.Begin with the checking at 'the difference down-bowing and up-bowing' on A and D string.

Celloは各々の半音で、チェロ胴体の中で振動する方向に個性があることがわかったので、さらに精度を上げて全体像を調べてみる。
この個性は個々の楽器に依存する問題であるが同時にチェロという楽器の構造に共通する現象と考えられる。
具体的進め方は次りとおりとする。
1.Celloの胴体の輪切りレベルを(角度=)0度として、振動方向を反時計回り角度で表示する。
2.水平方向マイク・垂直方向マイクの波形により、相のズレ(マイクへの音の到達遅延)がわかるので逆算すれば振動方向が計算できるはずである。
それぞれのマイクへの到達時間は、EXCEL関数では =COS( ) または =SIN( )関数で求められ、Vマイク - Hマイク の時間差も同じくサイン曲線であるので、振動方向は =ACOS(遅れ/(測定音の周期/2))... のイメージで求められるはずである。
3.現実には、測定するCelloの設置角度は水平から45度でなく、65度程度であるので、この角度差を補正する。
4.これにより音ごとの個性的な振動方向(音の飛び方向)の概要がわかるはずである。しかし、実際には、チェロの構造上の関係もあって複雑な波形の組み合わせをとることもあるし、床やエンドピンの共振の影響で方位がゆがめられたり波形がつぶれたりして明確な計算ができない場合もある。明確に方位を得られない場合は、後日手法を改良して挑戦することにする。振動している場所も推定できるかもしれない。少なくとも知識は増えるだろう。
5.まず最初に、A線・D線上の音について、ダウン弓とアップ弓で、振動方位に差があるかチェックしてみよう。