567. Response and Newton's laws of motion

 [ 10/10/2020 ]     Labels:  75.Resonance

 
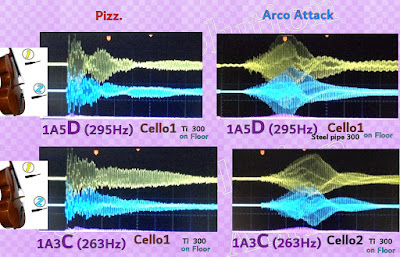
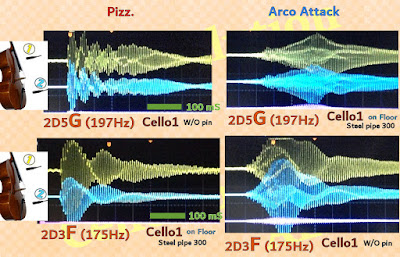
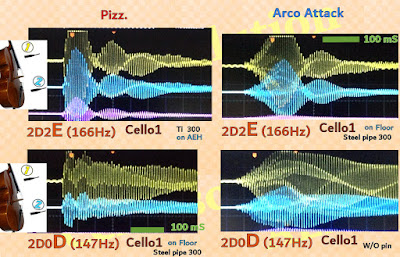
The resonance mechanism around cello endpin(and tailpiece) seems having something in common especially at tones on D, G and C string.
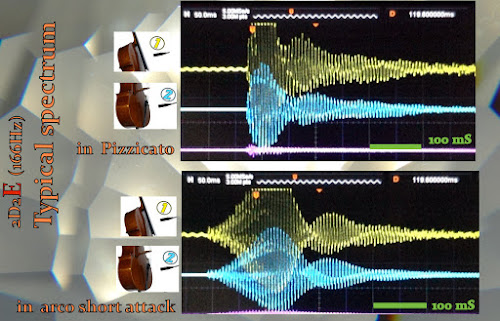
1- In many cases, accessories(endpin or tailpiece) resonate few after a pizzicato-pluck. This behavior reminds us of the Newton's first law - Every object persists in uniform motion -. Another saying, an endpin might rather work as a mute against momentary force/vibration.
2- On the other hands, endpins often resonate with arco-bowed tones. When the energy is supplied or the vibration is accelerated, moreover endpin tip is anchored on the floor, endpins resonates beyond expectations. This phenomenon also reminds us of the Newton's second law - Force equals mass times accelerations -. Many cellists get experience on their right hand an extra-resistance from cello strings, this action/re-action force must be the cause. The equation suggests the force is proportional to mass of material(or also may be to vibrating length of endpin).
3- The resonance intensity/amplitude of endpin often differs capriciously, and resonance mechanism seems different at high tones on A string. These issues will be studied later.

測定した代表的な振幅データを見てみる。D線、G線、C線上の測定データについて共通点が見られた。
1.ピチカート時、エンドピンとテールピースはほとんど共振していない。ニュートンの運動の第一法則(慣性の法則) を連想するように、突然与えられて動きに対してエンドピンは静止状態を維持しようとしているかのようだ。つまり、衝撃・一過的振動に対してはどちらかと言えばミュート効果として働いているように見える。
2.ボーイング演奏の場合、または弓を使ったアタックの時は逆に(一般的に)大きく共振する場合が多い。つまりエネルギーが継続して供給される場合または加速される場合、エンドピンは強く共振する。ここではニュートンの第二法則( F = m * a )が連想される。チェロを床置きして弓演奏する時、右手が受ける想定外の抵抗(F)はエンドピン等自体の運動エネルギーであり、エンドピンの質量(または振動している部分の長さ分の質量)に比例するように思われる。おそらくこれが重いレスポンスの正体である。
3.エンドピンやテールピースの振幅は常に同じではなく、時として気まぐれに変化する。ボーイングスキルとも関係すると思われるが、チェロの中を伝わっていくルートと関係があるだろう。また、A線領域のエンドピンの共振については、少し別のメカニズムが存在しているように思われる。(後日スタディー予定)

566. Response-Resonance Measurement Point

 [ 10/02/2020 ]     Labels:  75.Resonance

 
Currently 1500 measurements (or more) have been carried on about the response/resonance of cello.
Measurement points on/for cello are following four positions :
-1: around 10 to 15 cm over upper hemisphere of top-plate ( by small sound microphone )
-2: around 10 to 15 cm over bottom hemisphere of top-plate ( by small sound microphone )
-3: on tailpiece, a tuner microphone is held on by a rubber band as a same manner.
-4: on endpin tip, another tuner microphone is held on by a rubber band as a same manner.

It is unfair to compare directly the amplitude between audio microphones and tuner(contact) microphones, however the results are very acceptable because the result amplitude reminds us the feeling when our fingers actually touched at top-plate, tailpiece and endpin.
A number of planned measurements, the conditions are attached below, will probably finally show us a rough overall picture of response/resonance of cello: which tone, which condition makes endpin/tailpiece resonate, when and why.

測定機器とマイクの設定を改めて統一して、ともかく多数・広範囲に測定して、チェロのレスポンスと共振状態の全体像を調べている。
これにより、どの音がどう響いているか、床との関係でチェロの響きが変化するのか、エンドピンとテールピースが何時共振しているのか、全体像が見えるはずである。
この一連の測定で改めて注意・見直した点は次の通りである。
(1)測定点はわかりやすいように上から下へ、①表板上部の10-15cm上、②表板下部の10-15cm上、③テールピース、④エンドピン先端 の順とした。　(エンドピン無の場合は、④=テールピン直下を測定)
(2)①②の音声マイクは直近の表板の振動をとらえいてるはずである。なぜなら表板の物理的振動速度に比べて空中の音速は 100倍以上に高速であるから。
③④のチューナーマイクはテールピースやエンドピンの物理的振動をとらえる。これらのアクセサリーは表面積が小さく重いためにそれ自身はほとんど音波を生成することは無い。①②と③④の振幅強度を直接比較するには無理があるが、指で触れば胴体もエンドピンも各々明確に振動していることが解る。この経験値は今回のオシロスコープの振幅と大きな違和感はない。
③④のチューナーマイクについては接触状態によって振幅に差がでることがあるので、ゴムバンドを使って同条件となるよう注意を払った。(3)測定者の右手の強度によって発生する音の振幅が変わるが、今回は絶対値ではなく、①②の平均値に対する③④の相対値を比較することとする。
現在 1500ケ 以上の測定が進行中である。

565. Cello Tone Portraits MEMO

[ 09/19/2020 ]      Labels: 61..Sound color-2

Typical tone portraits(oscilloscope waveform) of cello from C(66Hz) up to A(442Hz) have been posted up to now. These photos, oscilloscope's horizontal lattice was set as 50mS, show us two important facts.
(1) There is a regularity/resemblance in the tone portraits according to the tone name such as C,D,E,F,G,A,, when they are played by pizzicato, beyond octaves or cello instruments or endpins. This phenomenon is probably originated in the cello body structure and its dimensions.
(2) Cello seems to be able to create a single-beat waveform(noiseless, beautiful) for tones G(98Hz) and above. Skilled cello players can probably create such a simple waveform even on arco-tones. On the other hand, for low frequency notes(C:66Hz to F#:93Hz), cello body is too short to create such a long wavelength by its single-beat. When an endpin is not equipped, cello recruits some additional regular up-beats(1-4 times) by itself inside the body to make up a complete fundamental period. However if the endpin is anchored on the floor and given continuous energy, the long length wave goes through to endpin and rebounds at the floor, then brings back a noisy/interference vibration and reduces the original tone amplitude instead.
There seem to be a discontinuity fault in the resonance in and around G(98Hz) tone.
Here attached typical portrait photos of C(66Hz), G(98Hz) and D(147Hz) that are set H-lattice as 20mS to improve the resolution.

チェロの最低音(C,66Hz)からA(442Hz)までの主要音についてオシロスコープの波形(水平格子=50mS設定)を見てきた。ここでは２つの特徴があることに気づく。
(1) ピチカートから得られる共鳴波形は、音名ごとに極めて類似した姿をしている。これは、楽器が変わっても床とエンドピンの関係が変わってもあるいはオクターブが違っても共通に現れる類似形のようだ。つまり、チェロという構造・ディメンションからもたらされているように思われる。
(2) G(98Hz)以上の高音においては、全ての音でその音の基音周波数によるシンプルで美しい波形を得ることができるようだ。(厳密にはボーイング時においては一定のスキルは必要。)　しかし、低音のC-F#(C線上)においては基音のみの純粋な音を得ることができない。つまり、チェロ胴体が95Hz程度以下のシングルビートを作ることができないことを意味する。エンドピンが無い時は裏拍(1-4ケ、⇒倍音とも関係がある)を補足しながらその基音周期を形成している。エンドピンが装着され床に固定され、弓を使って連続してエネルギーが供給される場合、そのエネルギーは床に向かって(長周期を求めて)流れて行く。そのリバウンド波は規則的な裏拍を形成できないで雑音のようにフィードバックされ、C-F#ではその雑多な振動が混在する。
チェロは、G(98Hz)の上下で響きのルカニズムが異なっている。
添付の写真は、C(66Hz)、G(98Hz)、D(147Hz)の典型的な波形である。ここでは水平格子幅を20mSに拡大してある。C(66Hz)ではピチカートの場合、3-4ケの裏拍を伴って15mSの基音周期を形成しているのがわかる。

565. Cello Tone Portraits -A-

 [ 09/17/2020 ]      Labels:  61..Sound color-2,

565. Cello Tone Portraits -D-

 [ 09.14.2020 ]     Labels:  61..Sound color-2

565. Cello Tone Portraits -G-

 [ 09.14.2020 ]     Labels:  61..Sound color-2

565. Cello Tone Portraits -C-

 [ 09.14.2020 ]     Labels:   61..Sound color-2

56. Response TOPICS -2- Wolf tone

 [ 09/06/2020 ]      Labels: 61..Sound color-2,  63.Wolf tone

 
Many oscilloscope screenshots hint us a regularity in their resonance spectrum according to the tone name such as C,D,E,F,G,A,, only when they played by pizzicato. Each tone's spectrum shape seems very resembling beyond octaves or cello instruments.
The first two screenshots are typical E(166Hz, second semitone on D string) spectrum of pizzicato and short arco attack. They are all consisted of 6mS(E,166Hz) fundamental vibration and seem as if they are totally twisted or rolling.
The last two screenshots are very unique: E(almost 166Hz, 9th semitone on E string) wolf tone in pizzicato and arco long tone. The amplitude of wave regularly/irregularly dies away and recovers again.
Wolf tones probably relate to the simple/inflexible resonance of top-plate of cello.

オシロスコープで多くのCelloの音波形を見ていると、pizzicatoの波形は オクターブや楽器の違いとあまり関係なく C-D-E-F-G--等の音名ごとで極めてよく似ていることに気づく。例えば、E(166Hz, D線上第2半音)の典型的な波形は、最初の写真のようである。(上:ピチカート、下:短いアルコ・アタック)、6mSの基本周期で規則的に振動しながらねじれている(あるいはローリングしている)かのように見える。
下の写真は、その特殊なケースであるのウルフトーン(G線上の第9番半音付近で観察)をとらえたユニークな写真である。(上:ピチカートの中のウルフトーン、下:アルコの伸ばし音の中のウルフトーン)。途中一端振幅がゼロになっては復活している。
おそらくウルフトーンは表板のシンプルな振動と関連があり、厳格に左右対称に作られた楽器で起こりやすいのだろう。いづれもオシロスコープの水平格子幅は50mS。